Skip to contents

Calibration performance: ggplot version

valProbggplot.Rd

The function valProbggplot is an adaptation of val.prob from Frank Harrell's rms package, https://cran.r-project.org/package=rms. Hence, the description of some of the functions of valProbggplot come from the the original val.prob.

The key feature of valProbggplot is the generation of logistic and flexible calibration curves and related statistics. When using this code, please cite: Van Calster, B., Nieboer, D., Vergouwe, Y., De Cock, B., Pencina, M.J., Steyerberg, E.W. (2016). A calibration hierarchy for risk models was defined: from utopia to empirical data. Journal of Clinical Epidemiology, 74, pp. 167-176

Usage

valProbggplot(
  p,
  y,
  logit,
  group,
  weights = rep(1, length(y)),
  normwt = FALSE,
  pl = TRUE,
  smooth = c("loess", "rcs", "none"),
  CL.smooth = "fill",
  CL.BT = FALSE,
  lty.smooth = 1,
  col.smooth = "black",
  lwd.smooth = 1,
  nr.knots = 5,
  logistic.cal = FALSE,
  lty.log = 1,
  col.log = "black",
  lwd.log = 1,
  xlab = "Predicted probability",
  ylab = "Observed proportion",
  xlim = c(-0.02, 1),
  ylim = c(-0.15, 1),
  m,
  g,
  cuts,
  emax.lim = c(0, 1),
  legendloc = c(0.5, 0.27),
  statloc = c(0, 0.85),
  dostats = TRUE,
  cl.level = 0.95,
  method.ci = "pepe",
  roundstats = 2,
  riskdist = "predicted",
  size = 3,
  size.leg = 5,
  connect.group = FALSE,
  connect.smooth = TRUE,
  g.group = 4,
  evaluate = 100,
  nmin = 0,
  d0lab = "0",
  d1lab = "1",
  size.d01 = 5,
  dist.label = 0.01,
  line.bins = -0.05,
  dist.label2 = 0.04,
  cutoff,
  length.seg = 0.85,
  lty.ideal = 1,
  col.ideal = "red",
  lwd.ideal = 1,
  allowPerfectPredictions = FALSE,
  argzLoess = alist(degree = 2)
)

Arguments

p

predicted probability

y

vector of binary outcomes

logit

predicted log odds of outcome. Specify either p or logit.

group

a grouping variable. If numeric this variable is grouped into g.group quantile groups (default is quartiles). Set group=TRUE to use the group algorithm but with a single stratum for val.prob.

weights

an optional numeric vector of per-observation weights (usually frequencies), used only if group is given.

normwt

set to TRUE to make weights sum to the number of non-missing observations.

pl

TRUE to plot the calibration curve(s). If FALSE no calibration curves will be plotted, but statistics will still be computed and outputted.

smooth

"loess" generates a flexible calibration curve based on loess, "rcs" generates a calibration curves based on restricted cubic splines (see rcs and rcspline.plot), "none" suppresses the flexible curve. We recommend to use loess unless N is large, for example N>5000. Default is "loess".

CL.smooth

"fill" shows pointwise 95% confidence limits for the flexible calibration curve with a gray area between the lower and upper limits, TRUE shows pointwise 95% confidence limits for the flexible calibration curve with dashed lines, FALSE suppresses the confidence limits. Default is "fill".

CL.BT

TRUE uses confidence limits based on 2000 bootstrap samples, FALSE uses closed form confidence limits. Default is FALSE.

lty.smooth

the linetype of the flexible calibration curve. Default is 1.

col.smooth

the color of the flexible calibration curve. Default is "black".

lwd.smooth

the line width of the flexible calibration curve. Default is 1.

nr.knots

specifies the number of knots for rcs-based calibration curve. The default as well as the highest allowed value is 5. In case the specified number of knots leads to estimation problems, then the number of knots is automatically reduced to the closest value without estimation problems.

logistic.cal

TRUE plots the logistic calibration curve, FALSE suppresses this curve. Default is FALSE.

lty.log

if logistic.cal=TRUE, the linetype of the logistic calibration curve. Default is 1.

col.log

if logistic.cal=TRUE, the color of the logistic calibration curve. Default is "black".

lwd.log

if logistic.cal=TRUE, the line width of the logistic calibration curve. Default is 1.

xlab

x-axis label, default is "Predicted Probability".

ylab

y-axis label, default is "Observed proportion".

xlim, ylim

numeric vectors of length 2, giving the x and y coordinates ranges (see xlim and ylim).

m

If grouped proportions are desired, average no. observations per group

g

If grouped proportions are desired, number of quantile groups

cuts

If grouped proportions are desired, actual cut points for constructing intervals, e.g. c(0,.1,.8,.9,1) or seq(0,1,by=.2)

emax.lim

Vector containing lowest and highest predicted probability over which to compute Emax.

legendloc

if pl=TRUE, list with components x,y or vector c(x,y) for bottom right corner of legend for curves and points. Default is c(.50, .27) scaled to lim. Use locator(1) to use the mouse, FALSE to suppress legend.

statloc

the "abc" of model performance (Steyerberg et al., 2011)-calibration intercept, calibration slope, and c statistic-will be added to the plot, using statloc as the upper left corner of a box (default is c(0,.85). You can specify a list or a vector. Use locator(1) for the mouse, FALSE to suppress statistics. This is plotted after the curve legends.

dostats

specifies whether and which performance measures are shown in the figure. TRUE shows the "abc" of model performance (Steyerberg et al., 2011): calibration intercept, calibration slope, and c-statistic. TRUE is default. FALSE suppresses the presentation of statistics in the figure. A c() list of specific stats shows the specified stats. The key stats which are also mentioned in this paper are "C (ROC)" for the c statistic, "Intercept" for the calibration intercept, "Slope" for the calibration slope, and "ECI" for the estimated calibration index (Van Hoorde et al, 2015). The full list of possible statistics is taken from val.prob and augmented with the estimated calibration index: "Dxy", "C (ROC)", "R2", "D", "D:Chi-sq", "D:p", "U", "U:Chi-sq", "U:p", "Q", "Brier", "Intercept", "Slope", "Emax", "Brier scaled", "Eavg", "ECI". These statistics are always returned by the function.

cl.level

if dostats=TRUE, the confidence level for the calculation of the confidence intervals of the calibration intercept, calibration slope and c-statistic. Default is 0.95.

method.ci

method to calculate the confidence interval of the c-statistic. The argument is passed to auc.nonpara.mw from the auRoc-package and possible methods to compute the confidence interval are "newcombe", "pepe", "delong" or "jackknife". Bootstrap-based methods are not available. The default method is "pepe" and here, the confidence interval is the logit-transformation-based confidence interval as documented in Qin and Hotilovac (2008). See auc.nonpara.mw for more information on the other methods.

roundstats

specifies the number of decimals to which the statistics are rounded when shown in the plot. Default is 2.

riskdist

Use "calibrated" to plot the relative frequency distribution of calibrated probabilities after dividing into 101 bins from lim[1] to lim[2]. Set to "predicted" (the default as of rms 4.5-1) to use raw assigned risk, FALSE to omit risk distribution. Values are scaled so that highest bar is 0.15*(lim[2]-lim[1]).

size, size.leg

controls the font size of the statistics (size) or plot legend (size.leg). Default is 3 and 5, respectively.

connect.group

Defaults to FALSE to only represent group fractions as triangles. Set to TRUE to also connect with a solid line.

connect.smooth

Defaults to TRUE to draw smoothed estimates using a line. Set to FALSE to instead use dots at individual estimates

g.group

number of quantile groups to use when group is given and variable is numeric.

evaluate

number of points at which to store the lowess-calibration curve. Default is 100. If there are more than evaluate unique predicted probabilities, evaluate equally-spaced quantiles of the unique predicted probabilities, with linearly interpolated calibrated values, are retained for plotting (and stored in the object returned by val.prob.

nmin

applies when group is given. When nmin \(> 0\), val.prob will not store coordinates of smoothed calibration curves in the outer tails, where there are fewer than nmin raw observations represented in those tails. If for example nmin=50, the plot function will only plot the estimated calibration curve from \(a\) to \(b\), where there are 50 subjects with predicted probabilities \(< a\) and \(> b\). nmin is ignored when computing accuracy statistics.

d0lab, d1lab

controls the labels for events and non-events (i.e. outcome y) for the histograms. Defaults are d1lab="1" for events and d0lab="0" for non-events.

size.d01

controls the size of the labels for events and non-events. Default is 5.

dist.label

controls the horizontal position of the labels for events and non-events. Default is 0.01.

line.bins

controls the horizontal (y-axis) position of the histograms. Default is -0.05.

dist.label2

controls the vertical distance between the labels for events and non-events. Default is 0.03.

cutoff

puts an arrow at the specified risk cut-off(s). Default is none.

length.seg

controls the length of the histogram lines. Default is 0.85.

lty.ideal

linetype of the ideal line. Default is 1.

col.ideal

controls the color of the ideal line on the plot. Default is "red".

lwd.ideal

controls the line width of the ideal line on the plot. Default is 1.

allowPerfectPredictions

Logical, indicates whether perfect predictions (i.e. values of either 0 or 1) are allowed. Default is FALSE, since we transform the predictions using the logit transformation to calculate the calibration measures. In case of 0 and 1, this results in minus infinity and infinity, respectively. if allowPerfectPredictions = TRUE, 0 and 1 are replaced by 1e-8 and 1 - 1e-8, respectively.

argzLoess

a list with arguments passed to the loess function

Value

An object of type ggplotCalibrationCurve with the following slots:

call

the matched call.

ggPlot

the ggplot object.

stats

a vector containing performance measures of calibration.

cl.level

the confidence level used.

Calibration

contains the calibration intercept and slope, together with their confidence intervals.

Cindex

the value of the c-statistic, together with its confidence interval.

warningMessages

if any, the warning messages that were printed while running the function.

CalibrationCurves

The coordinates for plotting the calibration curves.

Details

When using the predicted probabilities of an uninformative model (i.e. equal probabilities for all observations), the model has no predictive value. Consequently, where applicable, the value of the performance measure corresponds to the worst possible theoretical value. For the ECI, for example, this equals 1 (Edlinger et al., 2022).

Note

In order to make use (of the functions) of the package auRoc, the user needs to install JAGS. However, since our package only uses the auc.nonpara.mw function which does not depend on the use of JAGS, we therefore copied the code and slightly adjusted it when method="pepe".

References

Edlinger, M, van Smeden, M, Alber, HF, Wanitschek, M, Van Calster, B. (2022). Risk prediction models for discrete ordinal outcomes: Calibration and the impact of the proportional odds assumption. Statistics in Medicine, 41( 8), pp. 1334– 1360

Qin, G., & Hotilovac, L. (2008). Comparison of non-parametric confidence intervals for the area under the ROC curve of a continuous-scale diagnostic test. Statistical Methods in Medical Research, 17(2), pp. 207-21

Steyerberg, E.W., Van Calster, B., Pencina, M.J. (2011). Performance measures for prediction models and markers : evaluation of predictions and classifications. Revista Espanola de Cardiologia, 64(9), pp. 788-794

Van Calster, B., Nieboer, D., Vergouwe, Y., De Cock, B., Pencina M., Steyerberg E.W. (2016). A calibration hierarchy for risk models was defined: from utopia to empirical data. Journal of Clinical Epidemiology, 74, pp. 167-176

Van Hoorde, K., Van Huffel, S., Timmerman, D., Bourne, T., Van Calster, B. (2015). A spline-based tool to assess and visualize the calibration of multiclass risk predictions. Journal of Biomedical Informatics, 54, pp. 283-93

Examples


# Load package
library(CalibrationCurves)
set.seed(1783)

# Simulate training data
X      = replicate(4, rnorm(5e2))
p0true = binomial()$linkinv(cbind(1, X) %*% c(0.1, 0.5, 1.2, -0.75, 0.8))
y      = rbinom(5e2, 1, p0true)
Df     = data.frame(y, X)

# Fit logistic model
FitLog = lrm(y ~ ., Df)

# Simulate validation data
Xval   = replicate(4, rnorm(5e2))
p0true = binomial()$linkinv(cbind(1, Xval) %*% c(0.1, 0.5, 1.2, -0.75, 0.8))
yval   = rbinom(5e2, 1, p0true)
Pred   = binomial()$linkinv(cbind(1, Xval) %*% coef(FitLog))

# Default calibration plot
valProbggplot(Pred, yval)

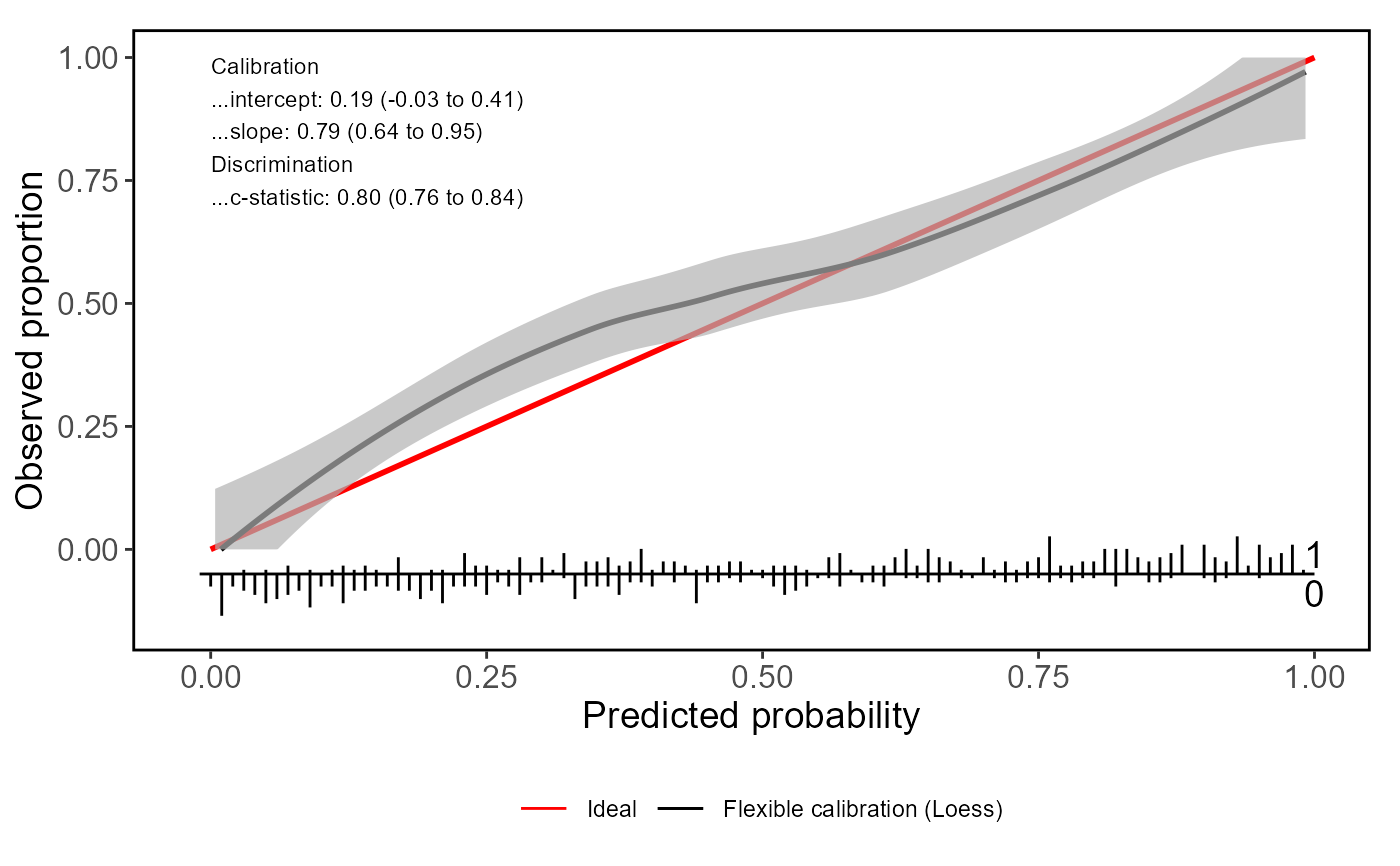#> Call:
#> valProbggplot(p = Pred, y = yval)
#> 
#> A 95% confidence interval is given for the calibration intercept, calibration slope and c-statistic. 
#> 
#>          Dxy      C (ROC)           R2            D     D:Chi-sq          D:p 
#>   0.60048690   0.80024345   0.35491505   0.30737619 154.68809420   0.00000000 
#>            U     U:Chi-sq          U:p            Q        Brier    Intercept 
#>   0.01384033   8.92016298   0.01156142   0.29353586   0.18549917   0.18828469 
#>        Slope         Emax Brier scaled         Eavg          ECI 
#>   0.79397043   0.08026282   0.25724275   0.05093656   0.37394083 

# Adding logistic calibration curves and other additional features
valProbggplot(Pred, yval, CL.smooth = TRUE, logistic.cal = TRUE, lty.log = 2,
 col.log = "red", lwd.log = 1.5)

#> Call:
#> valProbggplot(p = Pred, y = yval, CL.smooth = TRUE, logistic.cal = TRUE, 
#>     lty.log = 2, col.log = "red", lwd.log = 1.5)
#> 
#> A 95% confidence interval is given for the calibration intercept, calibration slope and c-statistic. 
#> 
#>          Dxy      C (ROC)           R2            D     D:Chi-sq          D:p 
#>   0.60048690   0.80024345   0.35491505   0.30737619 154.68809420   0.00000000 
#>            U     U:Chi-sq          U:p            Q        Brier    Intercept 
#>   0.01384033   8.92016298   0.01156142   0.29353586   0.18549917   0.18828469 
#>        Slope         Emax Brier scaled         Eavg          ECI 
#>   0.79397043   0.08026282   0.25724275   0.05093656   0.37394083 

valProbggplot(Pred, yval, CL.smooth = TRUE, logistic.cal = TRUE, lty.log = 9,
col.log = "red", lwd.log = 1.5, col.ideal = colors()[10], lwd.ideal = 0.5)

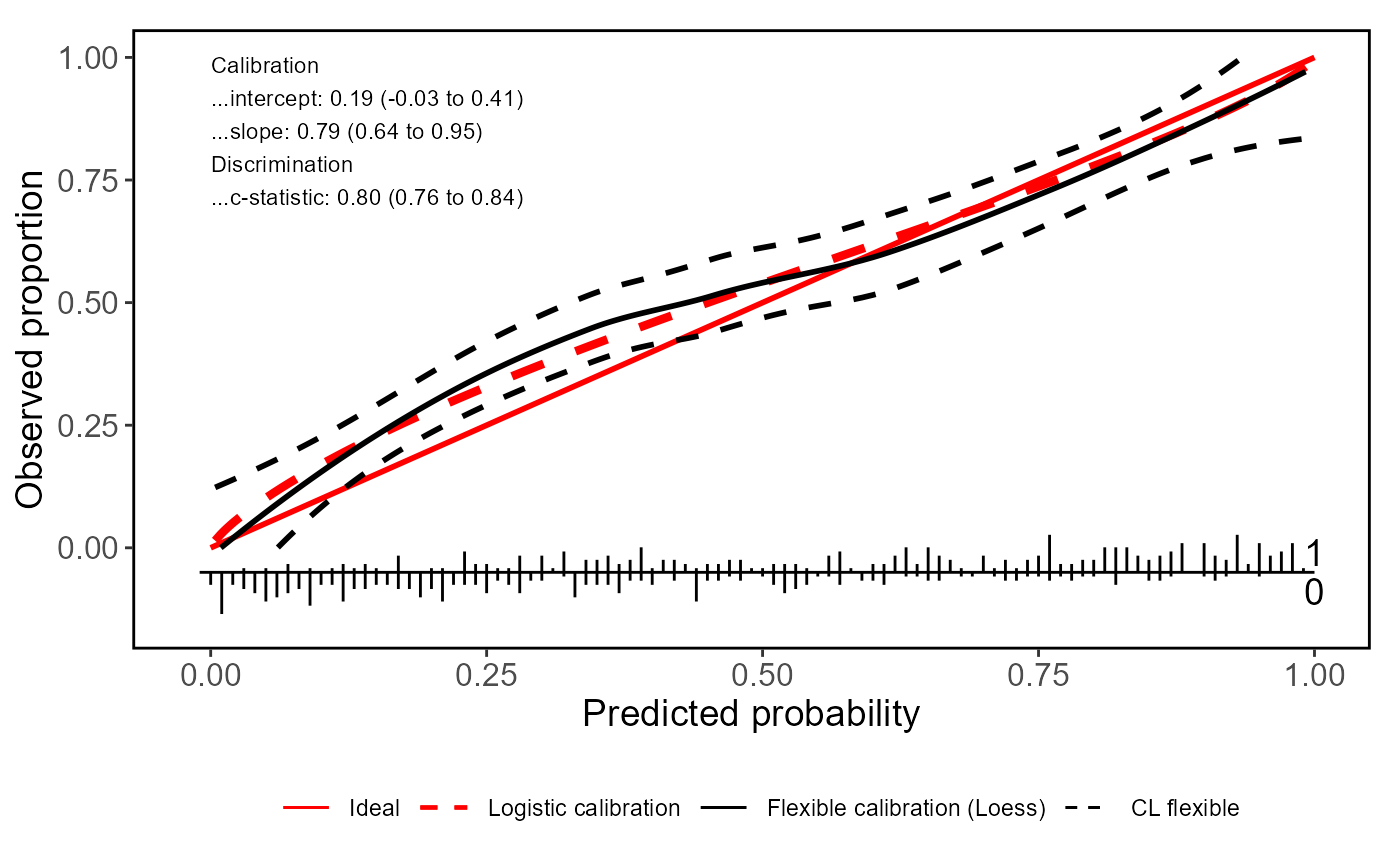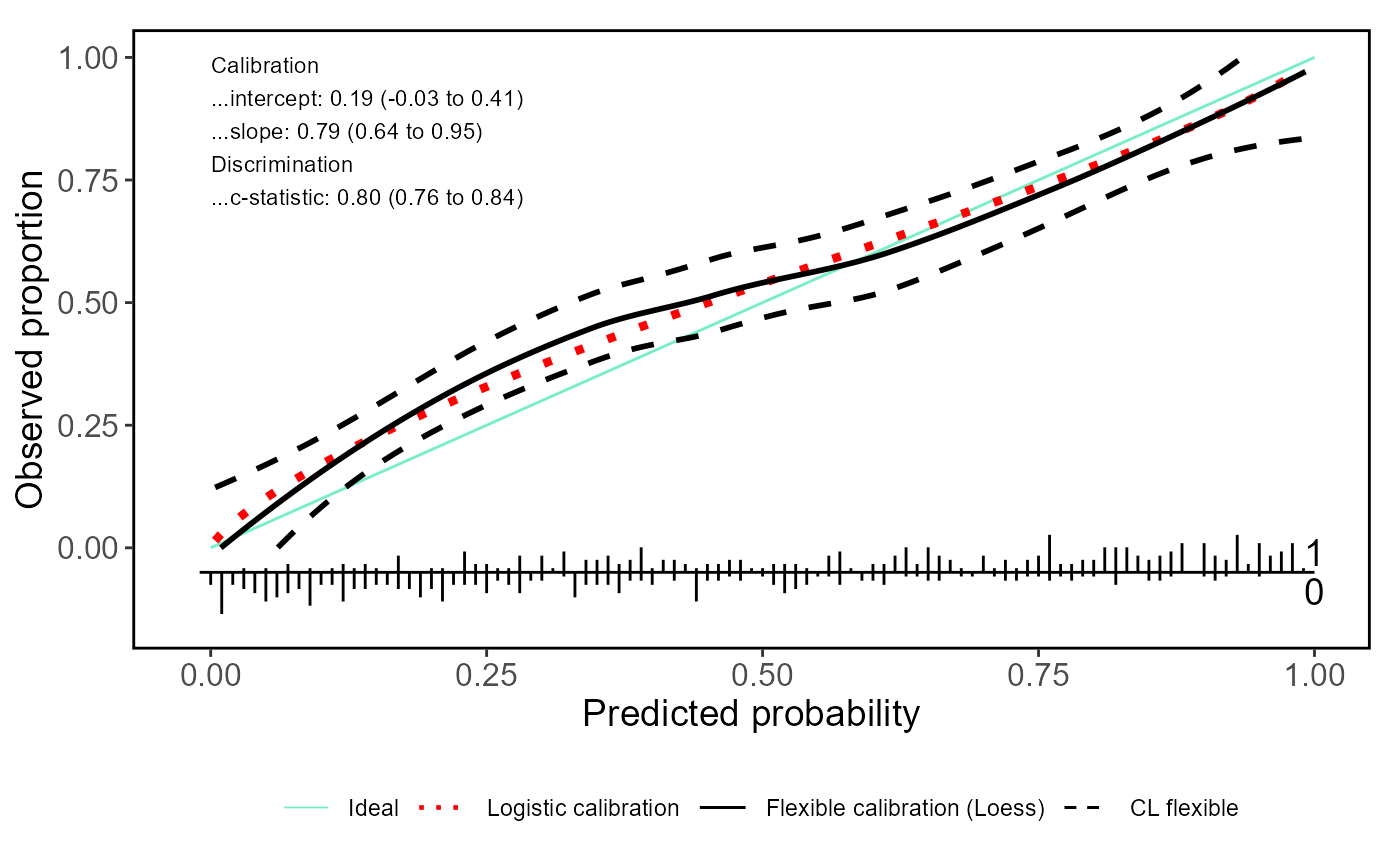#> Call:
#> valProbggplot(p = Pred, y = yval, CL.smooth = TRUE, logistic.cal = TRUE, 
#>     lty.log = 9, col.log = "red", lwd.log = 1.5, col.ideal = colors()[10], 
#>     lwd.ideal = 0.5)
#> 
#> A 95% confidence interval is given for the calibration intercept, calibration slope and c-statistic. 
#> 
#>          Dxy      C (ROC)           R2            D     D:Chi-sq          D:p 
#>   0.60048690   0.80024345   0.35491505   0.30737619 154.68809420   0.00000000 
#>            U     U:Chi-sq          U:p            Q        Brier    Intercept 
#>   0.01384033   8.92016298   0.01156142   0.29353586   0.18549917   0.18828469 
#>        Slope         Emax Brier scaled         Eavg          ECI 
#>   0.79397043   0.08026282   0.25724275   0.05093656   0.37394083